
Interesting graphics add new flavours to the Tetris classic
Mike Goldberg shows the versatility of the Archimedes by programming a simple Tetris look-alike
One of the most useful things about computers is their versatility - you can make it add your accounts up one day and save the universe the next if you should so desire.
With the current crop of fast processors and enormous memory capacities Acorn computers have become, in some respects, more obliging to the ordinary user.
From the personal programming point of view there is now no need to write your own machine code routines for fast screen output as most of these are taken care of by the built-in software and hardware, enabling us mere ordinary mortals to write very impressive software indeed.
Of course harnessing the full speed capabilities of these beasts is not our prime concern - but utilising what there is from Basic is. Combined with what we have looked at before we shall see how easy it is to create a complete game tailored to your own requirements.
Back in the good old BBC Micro days you may well have had a great idea for a game only to find that coding it produced the world's slowest, and therefore unplayable, junk. The solution then was assembly language and machine code, which to some of us was not as intuitive to use as Basic, but very rewarding if persevered with.
If that was not prohibitive enough for you, lack of memory certainly was - the compromises were always between that and different sprites and game levels.
Yet you can still hear the continued whining about the lack of memory on a 1Mb Acorn machine - how life preservingly essential it must be to create your own sprite handler, only necessary if you want to make a career out of software and own the company.
What nonsense! Tetris carried off all the trophies because it was a brilliantly original, simple, playable game requiring only a good grounding in writing Basic programs.
To prove it we will look at how easy it is to produce a version of our own, only adding extras to the game to identify it personally rather than improve it. This version is called CATtris, to keep my cat happy, and is on the cover disk.

Everyone on this planet must have seen one version or another of Tetris. Briefly, you fit different shapes together in a bucket forming lines which disappear but don't spill over the top. Succinct I think.
Each of the seven shapes is made up from four blocks - see below - and can be rotated through the four points of the compass.
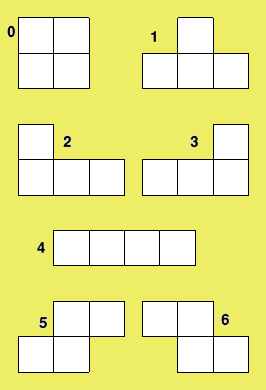
When a shape is dropped from the top of the bucket, the computer needs to know if it has hit an already occupied space or the bottom of the bucket.
We can see if something is going to strike another, but how do you tell the computer that something is there?
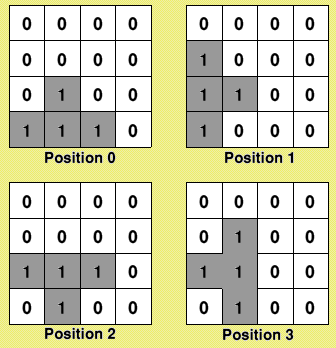
If you divide up the bucket area into squares the same size as the blocks from which the shapes are made, you can represent vacant squares as Os and occupied squares as 1s (see next picture). Store this data in an array:
G%(rows%,column%) = 0 or 1
To start with, all the squares are empty and have a value of 0. Note that the bucket is included in the grid system as this is the boundary and, therefore, all grid values are set to 1.
The idea is that when the shape lands, the grid squares it occupies become 1s. Subsequent shapes will now have to weave past, interconnect or land on this - but how does the computer know which shape and its orientation?
To print the correct shape on screen we must identify it and its orientation. Use a two-dimensional array thus:
S%(6,3) | | 0 | Orientation > 3 -+- 1 | 2 Which Shape
For example, S%(2,1) indicates shape 2 facing direction 1. The position of the shape within the grid is a simple matter of X, Y coordinates but this is most important.
Without knowing exactly where the shape is, none of the rest can be worked out. As the shape descends, the Y coordinate alters by 1.
Similarly, moving left or right alters the X coordinate by 1. But these are peculiar shapes with odd blocks here and there - how do you test for a collision like the one shown here?
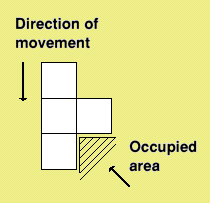
Create a three-dimensional array which contains this information:
H%(6,3,3) = Y offset | | | | | the 4 blocks (Left to | | right) 0 1 2 3 | | | shape orientation | Which shape
Look at Figure IV. The X, Y coordinate of the shape is always the bottom left and when testing for a collision below the shape we work across the shape left to right, block by block. The figures below each block tell you how far to look in the Y direction from the present Y coordinate.
A 0 would mean look at the grid the same Y coordinate as the shape, a 1 would mean look at the grid Y+1, that is the line below and so on. The -9 is indicates there is no block to check but any minus figure below -2 would have done.
So this checks underneath each of the four blocks to see if the grid has a block (stored as a 1) in it. If it has, there has been a collision and the shape stops. Obviously if no blocks (or is) are found, the shape continues to descend.
Left and right motion and rotation are dealt with separately as I felt that the shape always descends automatically but you move the shape in other directions. By treating each shape as a 4x4 grid with the blocks represented by 1s and the spaces as 0s it is easy to check what is moving where.
Q%(6,3,15) 0 1 2 3 | | | 4 5 6 7 | | 4x4 grid number > 8 9 10 11 | orientation 12 13 14 15 shape
For example, if you hit the key for moving right, the collision routine checks through all 16 parts of the 4x4 grid row by row checking each column, Figure VI. The position the shape is to move to is checked for occupation by other blocks as is the edge of the bucket.
If a 1 is found where a corresponding 1 of your shape is, the move is cancelled. Again, checking is done left to right and much more simply than my other routine now I think about it - this inevitably occurs as you progress through a program. More elegant and efficient routines naturally evolve as understanding sets in.
Once a shape has landed, the grid information needs to be updated to accommodate the new state of affairs. Where the shape's blocks reside determine which part of the grid array is altered to 1s and is simply a matter of comparing the shape's X, Y and 4x4 grid 1s and 0s with the X, Y of the bucket grid's rows and columns.
Checking for a complete line is now easy as all lines are tested for a complete row of is stored in the grid array. If a 0 is found, the rest of a line need not be tested as the 0 indicates a hole in it.
Working through each line from top to bottom is the correct order and if a line is found it is erased and the above shapes all move down a line. Here all the data held in the grid array is shifted similarly up to the where the line occurred.
Checking to see if a shape pokes over the top of the bucket is a simple X, Y check and that's all there is to it.
This is the second time I have written a Tetris-like game and it really only has two, maybe three, hardish bits to wrap your brain around. If you can do it once you can improve on it, and coupled with the 32-bit power the graphics can be whatever takes your fancy. Speed is no problem and using bankswitching the display can be seamless.
The point here is although the version I have written has some sensible bits, a few silly bits, some inelegant chunks of code and one or two ooh look mum bits, it all combines to make something that works. That'll do for me - if it works why mess about with it?
Anyway, someone else will always come along and do that for you!
Click here to download CATtris
| Source: | Acorn Computing - March 1993 |
| Publication: | Acorn Computing |
| Contributor: | Mike Goldberg |